GEO 325M/398M Numerical Modeling in the Geosciences

Jackson School of Geosciences - University of Texas at Austin

Project maintained by mhesse Hosted on GitHub Pages — Theme by mattgraham

Course Description

Covers numerical solution of dynamical problems arising in the solid earth geosciences. Entails development of individual codes in Matlab and application of codes to understanding heat transfer, wave propagation, elastic, and viscous deformations. Requires familiarity with Matlab.

Syllabus

Previous course projects:

The course content will be guided by a current research problem that typically leads to a scientific publication within the following year or two. In past classes we have worked on the following problems:

Spring 2018: Impact-induced cryovolcanism in Occator Crater on dwarf planet Ceres [paper 1] [paper 2]
Spring 2019: Transport of surface oxidants through Europa’s ice shell [paper 1]
Spring 2020: Convective upwelling in Europa’s ice shell [paper 1] [paper 2]
Spring 2021: Mars groundwater response to impact cratering [paper 1]
Spring 2022: Two-phase convection in Europa’s ice shell [paper submitted]
Spring 2023: Post-impact hydrothermal convection [paper almost done - so close, really!]
Spring 2024: Preferential flow in infiltration [paper in the works]
Spring 2025: Convection of high-pressure ice

Class rooom and time

Tue/Th 9:30am - 11:00am in JGB 3.120 in person

Office hours

Mon noon-1pm - Geophysics Dojo (JGB 4.216): Soraya’s and Mbarak’s office hours
Wed noon-1pm - Geophysics Dojo (JGB 4.216): Marc’s office hours

Additional course websites:

Piazza - Discussion board
Matlab Grader - Homework (need accept email!)
Canvas - Just for grades.

Matlab basics:

Here are some LiveScripts I prepared for the first class in 2018 that didn’t have a Matlab prerequisite. If you don’t have much Matlab experience, please look through them. Vectorized programming is a particularly important topic.

demo_arrays.mlx [pdf]
demo_functions.mlx [pdf]
demo_control_flow.mlx [pdf]
demo_matlab_functions.mlx [pdf]
demo_plotting.mlx [pdf]
demo_vectorized_programing.mlx [pdf]
demo_odds_ends.mlx [pdf] (structures, logical indexing, anonymous functions)

Below are two files that I have sometimes used for the demos in class. If you put them into the folder with class files you should have no problem.

This years course project

In spring 2025 we will develop a model for the convection in high-pressure ice in icy ocean worlds that may controll the transfer of nutrients from the rocky interior into the ocean sandwiched between the layers of high and low pressure ice.

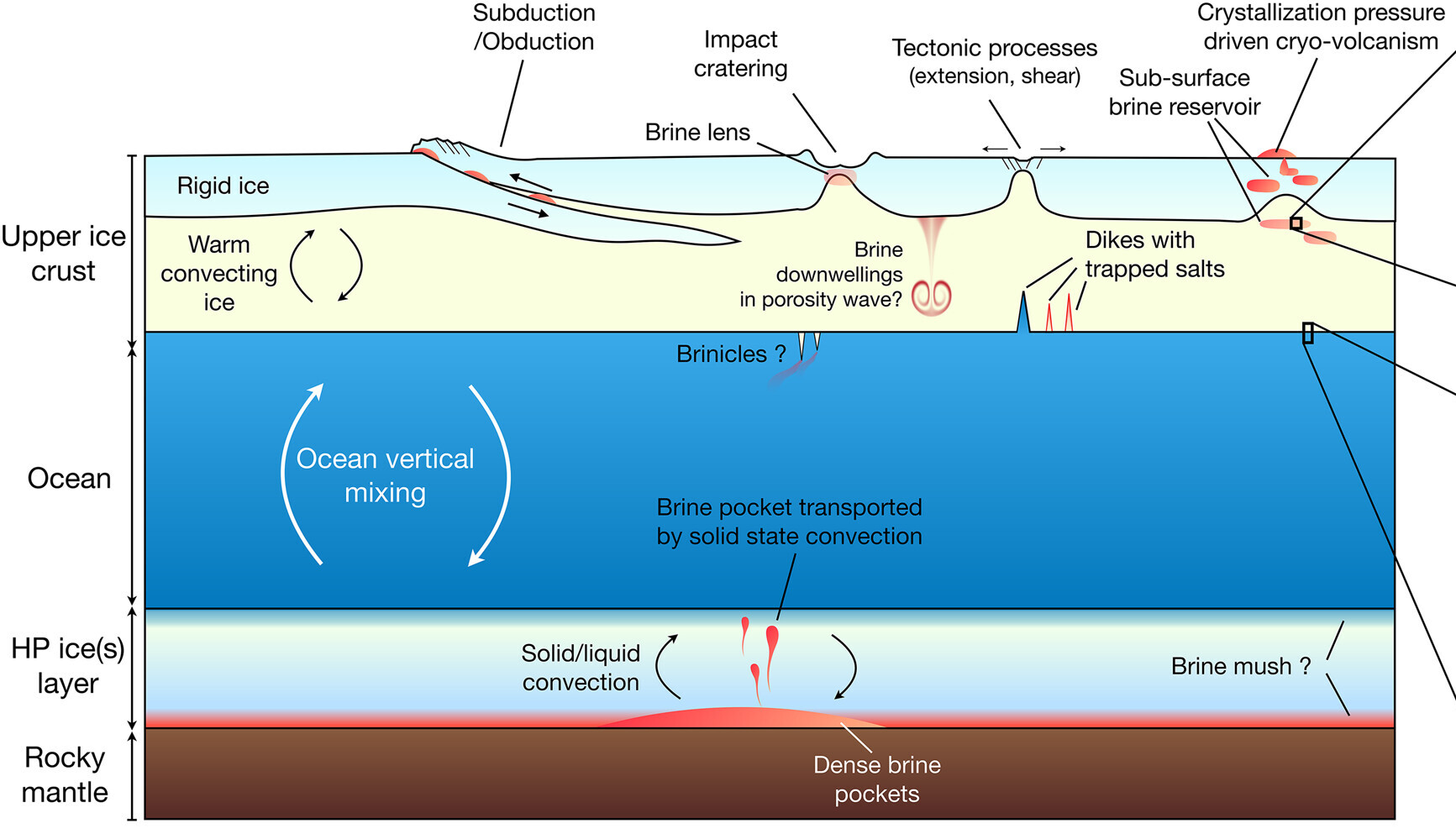
For reference see [Vance at al. 2020]

Introduction

Lecture 1 (Jan 14): Course Project and Conservation Laws

Intro slides, Class project
Notes: Balance Laws, Energy Balance

Lecture 2 (Jan 16): Introduction to numerics

Lecture: recording, board
Notes: Intro to Finite Differences,
LiveScripts: Finite Differences [script] [pdf],

Lecture 3 (Jan 21): Conservative Finite Differences

Lecture: recording, board
Notes: Consrevative Finite Differences
Live Scripts: Volcanic Conduit Heat Flow [script], [pdf]

1D Heat Flow

Lecture 4 (Jan 23): Discrete Operators

Notes: Discrete operators in 1D
Live Scripts: Discrete operators 1D [script] [pdf]

Lecture 5 (Jan 28): Boundary Conditions I: Dirichlet homogeneous

Notes: Dirichlet BC’s

Lecture 6 (Jan 30): Boundary Conditions II: Dirichlet heterogenous

Notes: Dirichlet BC’s - same as lecture 5
Live Scripts: Geotherm with Dirichlet BC’s [script], [pdf]

Lecture 7 (Feb 4): Boundary Conditons III: Neumann

Notes: Neuman BC’s, Compute Fluxes, Conservative Source
Live Scripts: Geotherm with mixed BC’s [script], [pdf]

Lecture 8 (Feb 6): Heterogenous coefficients and layered media

Notes: Layered Media, Variable coefficients
Live Scripts: Layered Media [script] [pdf], Variable coefficients [script] [pdf]

Lecture 9 (Feb 11): Non-linear problems and Netwon-Raphson method

Notes: Steady non-linear heat conduction, Newton-Raphson method
Live Scripts: Europa ice shell [script] [pdf], Newton-Raphson iteration [script] [pdf]

Lecture 10 (Feb 13): Numerical Jscobian

Notes: Numerical Jacobian
Live scripts: Numerical Jacobian [script] [pdf]

Lecture 11 (Feb 18): Analytic Jacobian

Notes: Analytical Jacobian
Live script: Analytic Jacobian [script] [pdf]

Lecture 12 (Feb 20): Transient heat transport

Lecture: Transcript, video
Time stepping: [LiveScript [pdf]
Planetesimal Thermal Evolution: [LiveScript] [pdf]

1D ADVECTIVE-CONDUCTIVE HEAT TRANSFER

Lecture 13 (Feb 25): Advective heat transport

Example: [LiveScript] [pdf]
Notes: Upwind method
LiveScripts: Advection in 1D [script] [pdf]
Discretization of Advection

Lecture 14 (Feb 27): Time stepping ADE

Discretization of Advection-Diffusion Equation: [LiveScript] [pdf]
Numerical Diffusion

DISCRETIZATION IN 2D

Lecture 15 (Mar 4): 2D Discrete operators - Part I

Notes: Discrete Operators
Live Scripts: 2D Matlab basics [script] [pdf], 2D Discrete Ops [script] [pdf]

Lecture 16 (Mar 6): 2D Discrete operators - Part II

Live Scripts: Transition 1D to 2D: [script], [pdf]

No class Mar 11!

Lecture 17 (Mar 13): 2D Advection matrix - Cooling of oceanic plates

Notes: Assembly of 2D advection matrix
Live Script: Cooling of the oceanic plate: [LiveScript] [pdf]

STOKES FLOW

Lecture 18 (Mar 25): Derivation of Stokes equation

Navier Stokes Equations, Scaling and reduction to Stokes Equation

Lecture 19 (Mar 27): Staggered grid for Stress/Strain

Staggered Grid and Discrete Operators
Live Script: Stokes grid and operators [LiveScript], [pdf]

no class Apr 1:

Lecture 20 (Apr 3): Discrete Stokes operators and BC’s

Discrete Stokes Operators
LiveScripts: Stokes BCs [script] [pdf],
Example: Lid-driven cavity (slip) [script] [pdf]